Somos Marcos Boj, Noemí Serrano y Nicolas Escribano de 1B
1. LETRAS EN VEZ DE NÚMEROS
1.1 ¿QUÉ ES EL ÁLGEBRA? ¿DE DÓNDE PROCEDE LA PALABRA ÁLGEBRA?
Son la parte de las matemáticas en la cual las operaciones aritméticas son generalizadas empleando números, letras y signos. Cada letra o signo representa simbólicamente un número u otra entidad matemática. Cuando alguno de los signos representa un valor desconocido se llama incógnita.
-La palabra «álgebra» es de origen árabe, deriva del tratado escrito por el matemático persa Muhammad ibn Musa al-Jwarizmi, titulado Al-Kitab al-Jabr wa-l-Muqabala
1.2 EJEMPLOS DONDE UTILIZAMOS EL ALGEBRA.
En tu ensayo solo hablalo como si lo estuvieras contanto a un amigo.
Se usa para simplificar las cosas, en vez de usar nombres largos los sustituimos por una letra, como en las tiendas, en vez de decir hice un pedido de 100 kilos de clorfenamina compuesta se puede decir 100 Kg de a
También para saber una cantidad o porcentaje de algo desconocido en relacón a otros, como una ecuación llamada comunmente regla de 3.
Y en general en cualquier ambito donde se requieren cálculos.
2.EXPRESIONES ALGEBRAICAS
2.1 ¿QUÉ ES UNA EXPRESIÓN ALGEBRAICA?
Una expresión algebraica es una combinación de letras, números y signos de operaciones. Las letras suelen representar cantidades desconocidas y se denominan variables o incógnitas. Las expresiones algebraicas nos permiten traducir al lenguaje matemático expresiones del lenguaje habitual.
2.2 MONOMIOS: ¿QUÉ ES UN MONOMIO?
Un monomio es una expresión algebraica en la que se utilizan letras, números y signos de operaciones. Las únicas operaciones que aparecen entre las letras son el producto y la potencia de exponente natural. Se denomina polinomio a la suma de varios monomios. Un monomio es un polinomio con un único término.
2.3 OPERACIONES CON MONOMIOS
Operaciones con monomios.
Suma de monomios.Para sumar dos monomios con la misma parte literal, se mantiene ésta y se suman los coeficientes. 
Resta de monomios.Para restar dos monomios con identica parte literal, mantenemos la parte literal y restamos los coeficientes. 
Suma de monomios
Sólo podemos sumar monomios semejantes.
La suma de los monomios es otro monomio que tiene la misma parte literal y cuyo coeficiente es la suma de los coeficientes.
axn + bxn = (a + b)xn
2x2 y3 z + 3x2 y3 z = 5x2 y3 z
Si los monomios no son semejantes se obtiene un polinomio.
2x2 y3 + 3x2 y3 z
Producto de monomios.Se multiplican los coeficientes y se suman los exponentes de los elementos con la misma base. 
aquí hay un video que tambien te lo explica como se hace si lo quiere ver pulse aquí
Cociente de monomios.Se dividen los coeficientes y se restan los exponentes de los elementos de la misma base. 
aquí hay un video que tambien te lo explica como se hace si lo quiere ver pulse aquí
PARTES DE MONOMIOS
El coeficiente del monomio es el número que aparece multiplicando a las variables.
La parte literal está constituida por las letras y sus exponentes.
El grado de un monomio es la suma de todos los exponentes de las letras o variables.
MONOMIOS SEMEJANTES
Son monomios semejantes aquellos en los que aparecen las mismas letras con los mismos exponentes.
3.- ECUACIONES
3.1 ¿QUE ES UNA ECUACION? DIFERENCIA ENTRE ECUACION E IDENTIDAD
Una ecuación es una igualdad entre dos expresiones algebraicas , denominadas miembros, en las que aparecen valores conocidos o datos , y desconocidos o incognitas , relacionados mediante operaciones matemáticas. Los valores conocidos pueden ser numeros, coeficientes o constantes; y también variables cuya magnitud se haya establecido como resultado de otras operaciones. Las incógnitas, representadas generalmente por letras, constituyen los valores que se pretende hallar.
DIFERENCIAS ENTRE IDENTIDAD Y ECUACION
Las ecuaciones son expresiones algebraicas con un signo igual
(igualdades literales) que solamente se verifican para algunos valores
de la letras, mientras que las identidades son las expresiones
algebraicas con signo igual (igualdades literales), que se verifican
para cualquier valor numérico de las letras.3.2 ELEMENTOS DE UNA ECUACIÓN
Los miembros de una ecuación son cada una de las expresiones que aparecen a ambos lados del signo igual.
Los términos de una ecuación son los sumandos que forman los miembros de una ecuación.
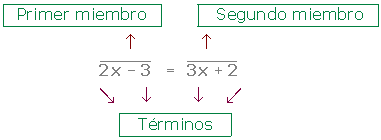
Las incógnitas de una ecuación son las letras que aparecen en la ecuación.


Las soluciones de una ecuación son los valores que deben tomar las letras para que la igualdad sea cierta.
El grado de una ecuación es el mayor de los grados de los monomios que forman sus miembros.
3.3 ECUACIONES EQUIVALENTES
Dos ecuaciones son equivalentes si tienen la misma solución.
2x − 3 = 3x + 2 x = −5
x + 3 = −2 x = −5
3.4 ¿que es resolver una ecuacion?
Ejemplo: Resolver la ecuación: 7x = 21
Para que la ecuación se mantenga igual, debes aplicar la misma operación a ambos lados de la ecuación. Si multiplicamos (o dividimos)un lado por una cantidad, debemos multiplicar (o dividir) el otro lado por la misma cantidad.
Esta ecuación se puede resolver dividiendo ambos lados por 7. La ecuación sería 7x/7 = 21/7. Esto se puede simplificar a x = 21/7 o x = 3.
Puedes verificar tu cálculo sustituyendo el valor de x en la ecuación original. (7*3=21).
Cómo
resolver ecuaciones de 1º Grado por Marcos Boj
1. hay que resolver los paréntesis: puede
haber varios tipos pero nosotros solo hemos estudiado dos 1.1-
ejemplo 1: 10-(8+2x)=3: en este tipo hay que resolver 1º el paréntesis pero
sino tiene la misma parte literal solo hay que quitar los paréntesis
quedaría así: 10-8-2x=3 (cambia los signos del paréntesis debido al signo
que hay delante del paréntesis, que es el de restar)
1.2-ejemplo 2: 2(x+3)=4 en este tipo hay que aplicar
la propiedad distributiva, es decir, hay que multiplicar el número que hay
delante del paréntesis por los que están dentro del paréntesis, quedaría así:
2x+6=4
2. hay que agrupar las "x" y los números:
3x+1+2-x=3x-4+x quedaría 2x+3=2x-4
3. hay que transportar que significa que hay que pasar
las "x" a la izquierda y los números a la derecha hagámoslo con el
ejemplo de antes: una vez agrupado solo hay que hacer esto: 3x-2x=-7
lo que esta sumando hay que restarlo a los dos miembro y al revés
con la resta que pasaría sumando
4. hay que resolver, es decir, hallar la solución, sigamos haciéndolo
con el ejemplo de antes: quedaría x = -7